1. 2D
Just for giggles, let’s see what happens if we use \(\sin\) and \(\cos\) to make 2D animations.
\[\begin{array}{rcl}
x(t) & = & \cos(2\pi t) \\
y(t) & = & \sin(2\pi t) \\
\end{array}\]
where \(t\) varies from \(0\) to \(1\).
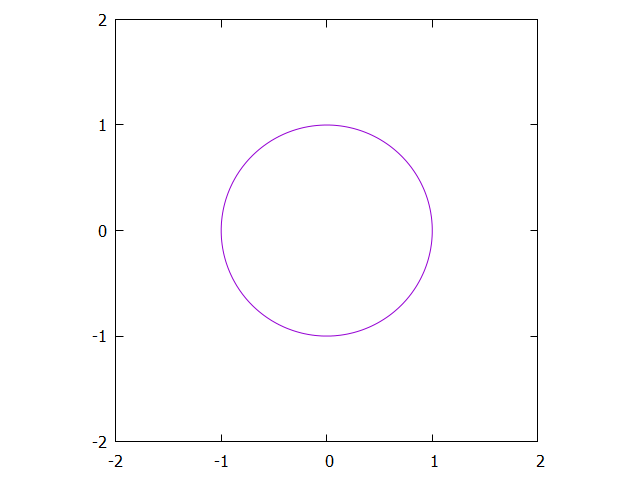
So, using that formula, we can make a shape move around in circles. We can experiment further by adding or changing some constants:
\[\begin{array}{rcl}
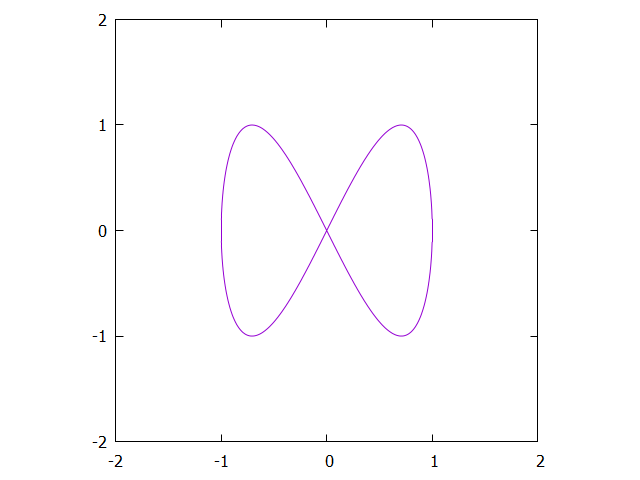
x(t) & = & \cos(2\pi t) \\
y(t) & = & \sin(4\pi t) \\
\end{array}\]
|
|
\[\begin{array}{rcl}
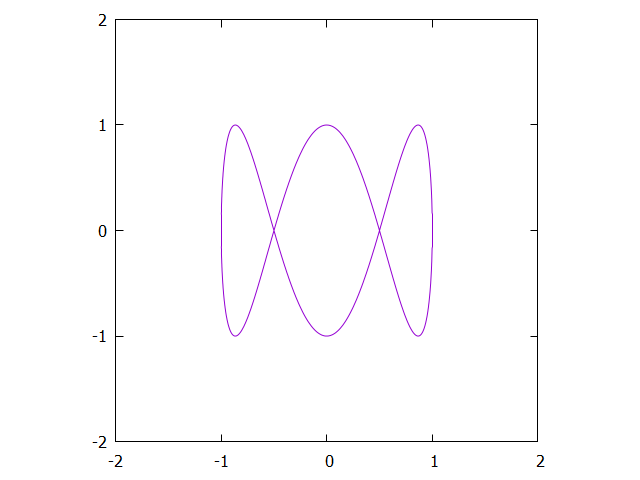
x(t) & = & \cos(2\pi t) \\
y(t) & = & \sin(6\pi t) \\
\end{array}\]
|
|
\[\begin{array}{rcl}
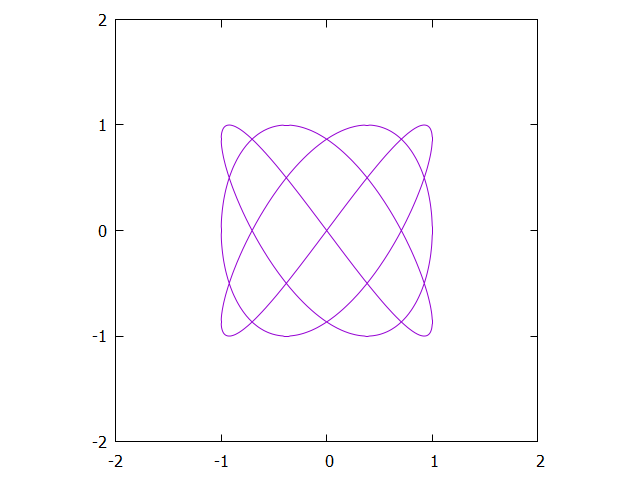
x(t) & = & \cos(6\pi t) \\
y(t) & = & \sin(8\pi t) \\
\end{array}\]
|
|
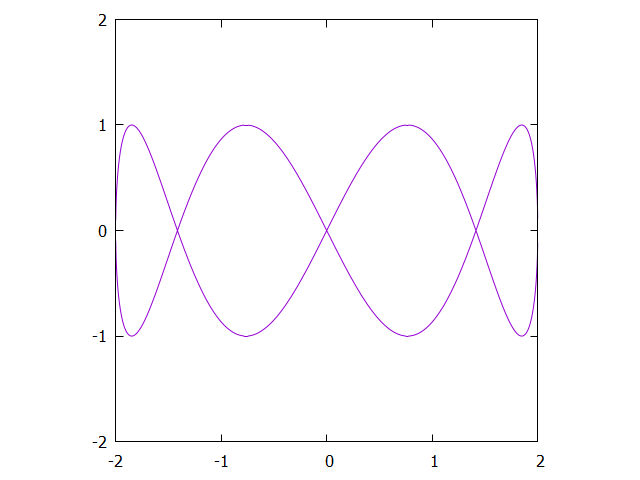
\[\begin{array}{rcl}
x(t) & = & 2 \cos(2 \pi t) \\
y(t) & = & \sin(8\pi t) \\
\end{array}\]
|
|
We can generalize these formulae to
\[\begin{array}{rcl}
x(t) & = & A \cdot \sin(B \cdot 2\pi \cdot t - C) \\
y(t) & = & D \cdot \sin(E \cdot 2\pi \cdot t) \\
\end{array}\]
where different choices for \(A\), \(B\), \(C\), \(D\) and \(E\) will yield different results.
|
Note
|
For those wondering about why the original formulae used \(\cos\) while the generalization uses \(\sin\): \(\sin(\alpha - \frac\pi2) = \cos(\alpha)\). |
2. 3D
We can do the same for three dimensions:
\[\begin{array}{rcl}
x(t) & = & A \cdot \sin(B \cdot 2\pi \cdot t) \\
y(t) & = & C \cdot \sin(D \cdot 2\pi \cdot t - E) \\
z(t) & = & F \cdot \sin(G \cdot 2\pi \cdot t - H) \\
\end{array}\]
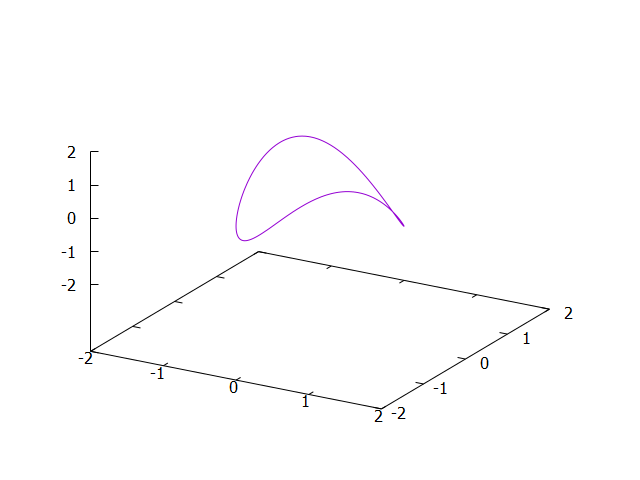
\[\begin{array}{rcl}
x(t) & = & \sin(2\pi t) \\
y(t) & = & \sin(2\pi t-\frac\pi2) \\
z(t) & = & \sin(4\pi t) \\
\end{array}\]
|
|
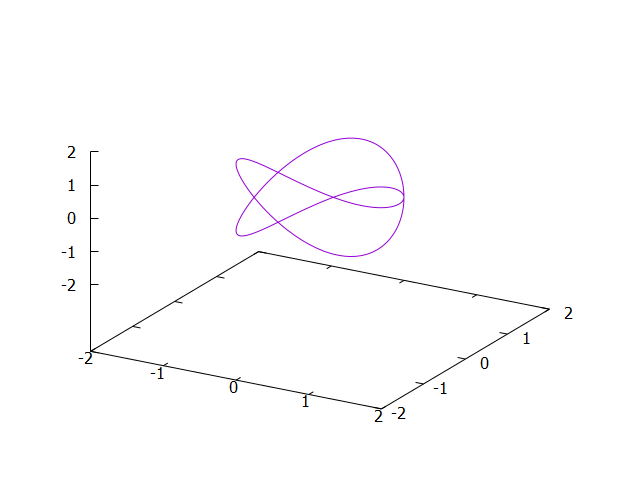
\[\begin{array}{rcl}
x(t) & = & \sin(4\pi t) \\
y(t) & = & \sin(4\pi t-\frac\pi2) \\
z(t) & = & \sin(6\pi t) \\
\end{array}\]
|
|
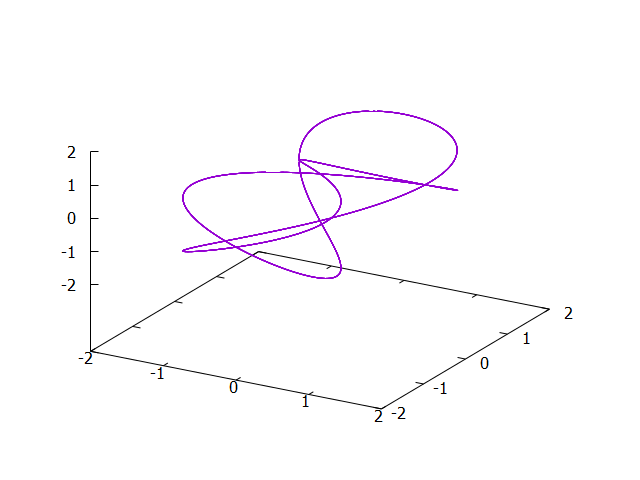
\[\begin{array}{rcl}
x(t) & = & \sin(8\pi t) \\
y(t) & = & 2 \sin(4\pi t-\frac\pi2) \\
z(t) & = & \sin(6\pi t) \\
\end{array}\]
|
|