1. Explanation
Diffuse light occurs when photons hit an uneven surface and are scattered around in all directions. With uneven, we mean uneven at the atomic level, which means that almost all surfaces can be said to be uneven. For the sake of simplicity, we will assume that photons bounce off the surface uniformly in all directions. For example, consider the white light source and the red surface:
With diffuse reflection, all non-red photons will be absorbed by the red surface while all the red ones will be reflected in random directions.
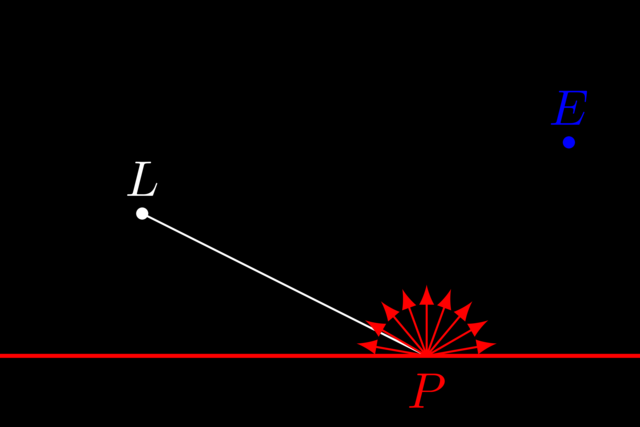
During ray tracing, we need to think backwards. We cast a ray originating in the eye \(E\). Say the ray hits the scene at some position \(P\). In order to determine the color of that hit, we need to determine two things:
-
What is the color of the photons going from \(P\) to \(E\)?
-
How many photons are going from \(P\) to \(E\)? This determines the brightness.
2. Determining the Color
The color of the photons arriving at \(E\) depends on two things:
-
What color photons does the light source \(L\) produce?
-
Which colors are reflected at \(P\)?
For example, if a white light (= all colors at once) shines on a green surface, you will perceive the surface as green as only the green photons get reflected. If red light shines on a blue surface, you won’t be able to see the surface as all photons are absorbed.
Since we use RGB values between 0 and 1, the "filtering" of photons can be easily achieved using multiplication:
If the light is white, i.e. RGB(1,1,1), and the surface is green, i.e. RGB(0,1,0), we get the reflected color by multiplying these colors together:
If the red light RGB(1,0,0) shines on a blue surface RGB(0,0,1), we get
3. Determining the Brightness
The number of photons depends on
-
How bright is the light itself? I.e. how many photons does the light \(L\) produce?
-
How many photons arrive at \(P\)?
-
How many photons are reflected at \(P\)?
So, there’s a certain amount of photons starting at \(L\), of which only a certain percentage reaches \(P\), of which only a certain percentage is reflected towards \(E\). Written mathematically, we get
3.1. Number of Photons Arriving at P
Let’s briefly switch to 2D to make explanations simpler. Consider the following figure:
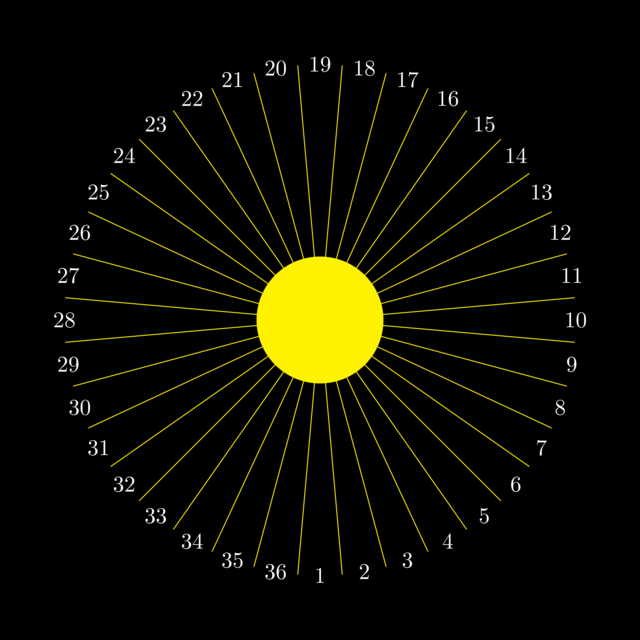
The light source emits light equally in all directions, i.e. 360° coverage. Let’s pretend the area light emits 360 photons. We divide these 360° in 36 angles of 10° each. Each of these segments contains the same amount of photons, namely 10. Let us now see what happens when these photons hit a surface.
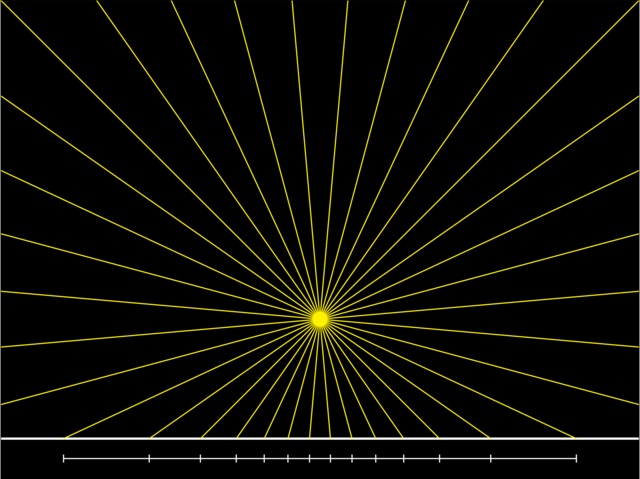
Notice how the area covered by the different 10° segments varies. The area right below the light is very small compared to those farther away on the plane. Given the fact that each area gets hits by the same amount of photons, this means that a small area is much brighter compared to the others due to the high concentration of photons.
How do we compute how many photons arrive at a given location? A good approximation is to look at the angle of the incoming light with respect to the surface.
To determine the brightness at a point \(P\), we take the normal unit vector on the surface at point \(P\), i.e. a vector that is perpendicular on the surface at \(P\). We measure the angle it makes with the incoming light.
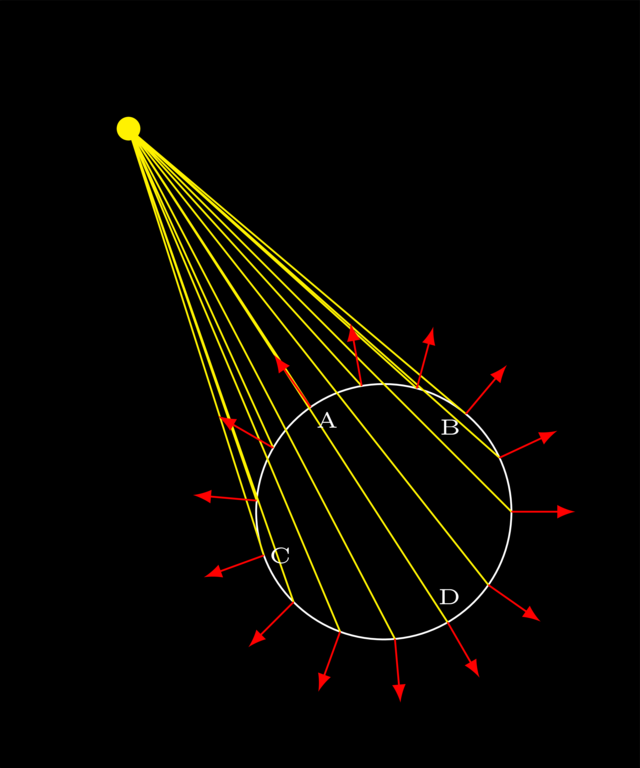
In point A, the normal and the photon’s direction are parallel. This is a point of maximal brightness. In points B and C, the light direction is perpendicular to the sphere’s normal at those points. You can imagine the photons grazing by, almost hitting the sphere, but not quite, meaning the brightness is zero.
What should happen at point D? The photons and normal are parallel, so is it a point of maximal brightness? Clearly it should not be: the light does not reach there and hence it should remain unlit. The solution is simple: you have to take the direction into account, not just the orientation. At A, the normal and the photons go in opposite directions, while at D, they point in the same direction.
All these rules are nice, but how do we put them in such a form that is easily implemented? The dot product comes to the rescue. Examine the following cases: the incoming light ray is represented by a yellow vector \(\vec i\), and the surface normal as a red vector \(\vec n\). It is important that both have length 1.
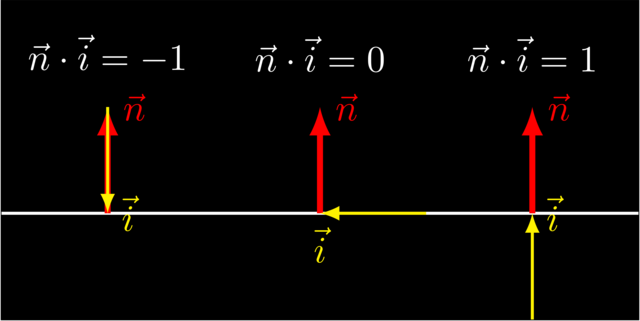
The dot product gives us almost exactly the values we need, namely it gives us the exact opposite value each time. We can solve this by simply flipping the sign.
4. Mathematics
To compute diffuse lighting, we need the following pieces of information:
-
The color \(C_\mathrm{L}\) of the light.
-
The position \(L\) of the light.
-
The location \(P\) of the point on a surface that we need to determine the color of.
-
The color \(C_\mathrm{S}\) of the surface’s material at \(P\).
-
The normal vector \(\vec n\) on the surface at \(P\).
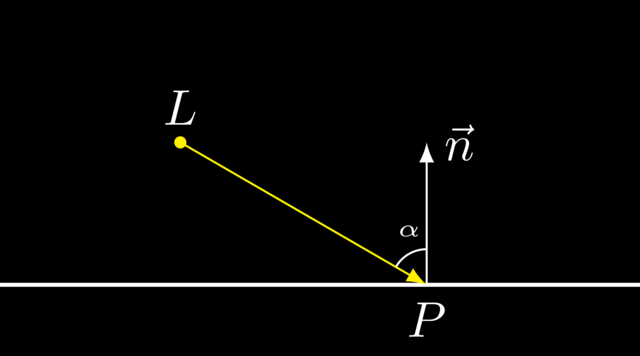
Compute the cosine of the angle \(\alpha\):
The amount of light reflected in each direction is then