1. Comparison
|
|
2. Explanation
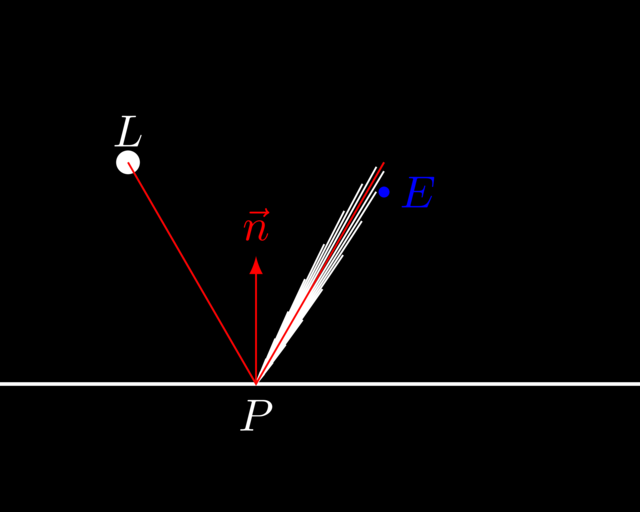
One peculiar thing about our RayTracer is that light sources are actually invisible. Consider the figure below:
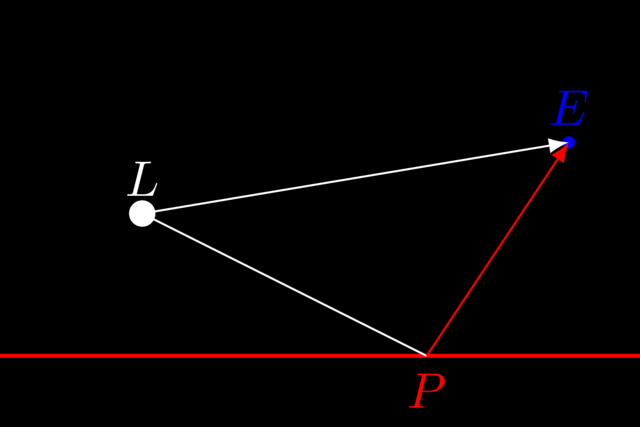
The light source \(L\) emits white photons. In reality, photons travel from \(L\) to our eye \(E\), making us perceive the light source as a bright white spot. In our implementation, however, only photons that travel from \(L\) to \(P\) to \(E\) are taken into account when rendering.
Specular highlights are the reflection of the light source in other objects. In a way, light sources are, in our implementation, the opposite of vampires: you can see their reflection in the mirror, but you cannot see them if you look straight at them.
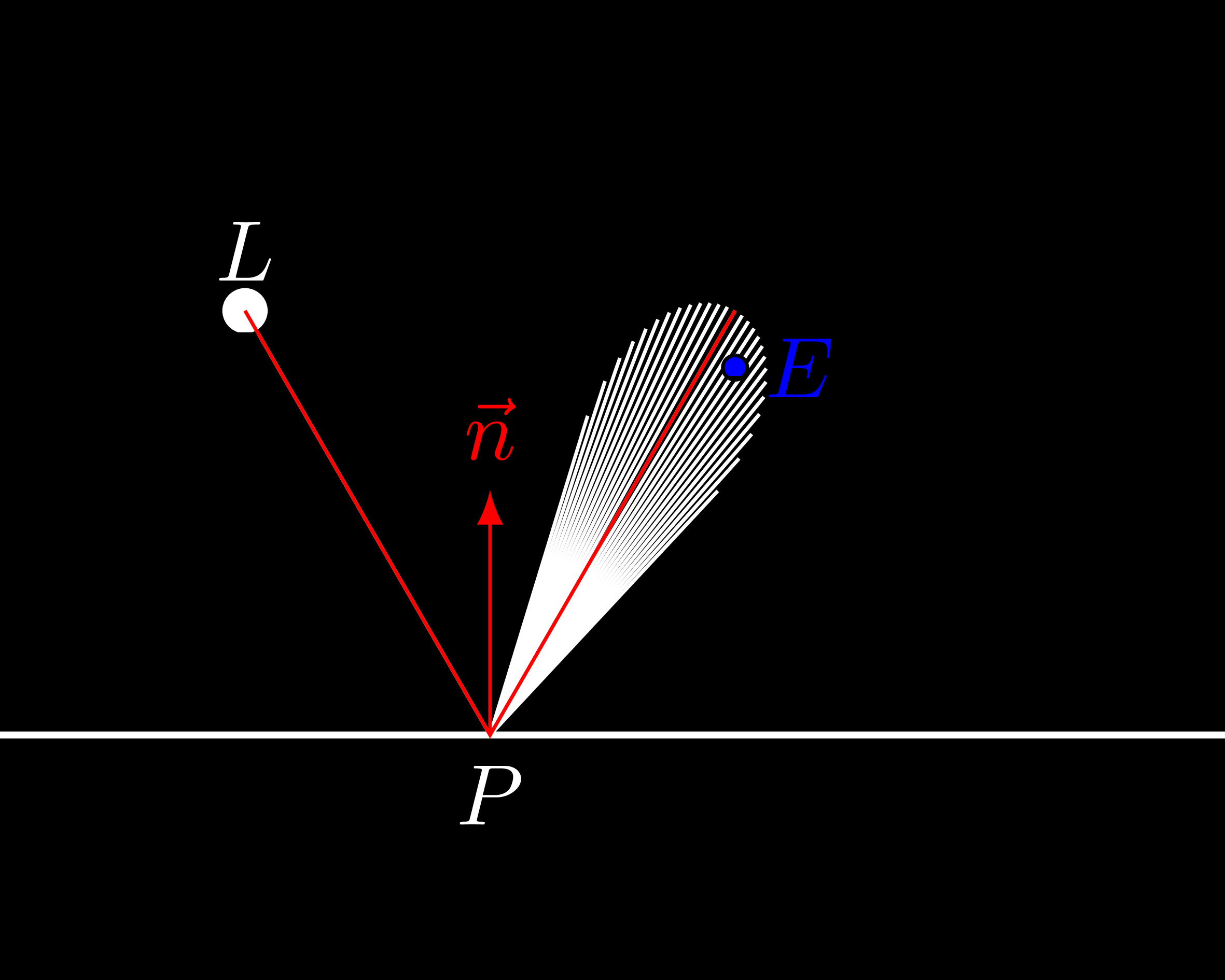
In the figure above, light arriving at \(P\) is reflected in a perfect mirrorlike fashion (i.e. not diffuse). This reflected beam of light flies by the eye \(E\), meaning we do not perceive it. If we were to only consider such perfect mirrorlike reflections, a point light would always be seen as a tiny dot, which is quite uninteresting. For this reason, we allow for a little bit of wiggle room.
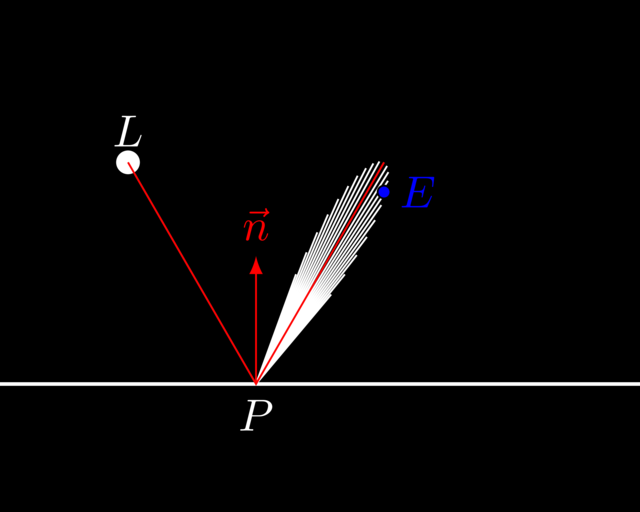
As shown on the figure above, the red line shows the "perfect" reflection. The white lines are "slightly off" reflections: the more they deviate from the one true reflection, the less photons they carry. How much deviation we allow is up to us.
|
|
|
|
|
|
3. Mathematics
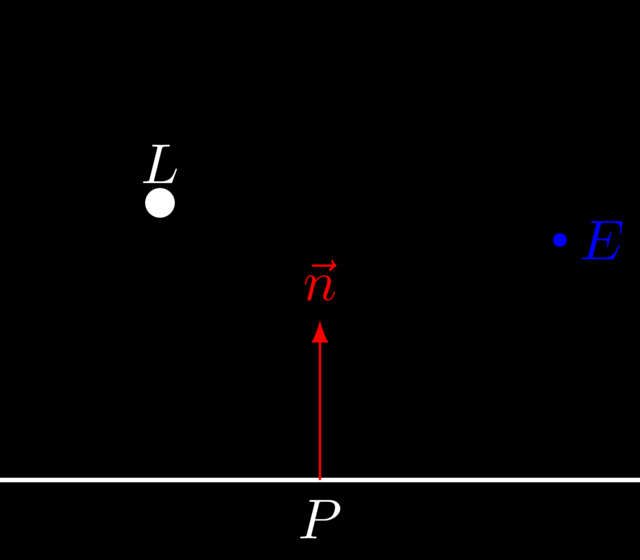
We need the following pieces of data:
-
The position of the light \(L\).
-
The color of the light \(C_\mathrm{L}\).
-
The hit position \(P\).
-
The material’s specular color \(C_\mathrm{P}\).
-
The eye’s position \(E\).
-
The specular exponent \(e\). This value determines the size of the specular highlight.
We perform the following steps:
-
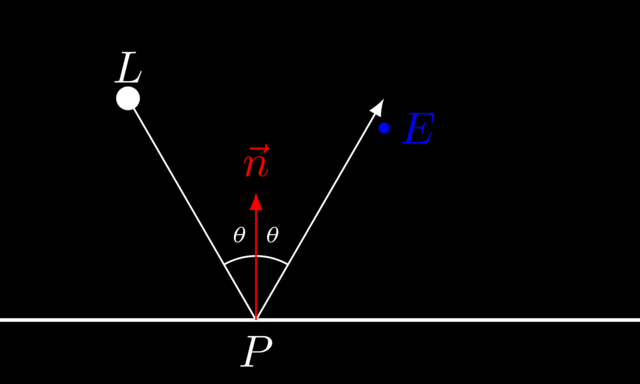
Compute the direction of the incoming light.
\[\vec{i} = \frac{P-L}{|P-L|}\] -
Compute the reflected direction.
\[\vec r = \vec i - 2 \cdot (\vec i \cdot \vec n) \cdot \vec n\] -
Compute the unit vector going from \(P\) to \(E\):
\[\vec v = \frac{E-P}{|E-P|}\] -
Compute the cosine of the angle between \(\vec r\) and \(\vec v\):
\[\cos \alpha = \vec v \cdot \vec r\] -
If \(\cos\alpha > 0\), the amount of photons reaching \(E\) from \(L\) is
\[C_\mathrm{L} \cdot C_\mathrm{P} \cdot \cos(\alpha)^e\]Otherwise, there is no specular highlight at location \(P\).