Cross Product

' '

Contrary to the dot product which resulted in a scalar, the cross product yields a vector, which can be found using the following formula:

\[ (x_1, y_1, z_1) \times (x_2, y_2, z_2) = (y_1 \cdot z_2-y_2 \cdot z_1, x_2 \cdot z_1-x_1 \cdot z_2, x_1 \cdot y_2 - x_2 \cdot y_1)\]

The resulting vector has the following characteristics:

\(\vec u \times \vec v\) is perpendicular to both \(\vec u\) and \(\vec v\).
The length of the resulting vector equals the product of the lengths of the operands times the sine of the angle they form.

\[|\vec u \times \vec v| = |\vec u| \cdot |\vec v| \cdot \sin(\theta)\]
Be careful: the cross product is not commutative: \(\vec u \times \vec v \neq \vec v \times \vec u\). We will expand upon this shortly.

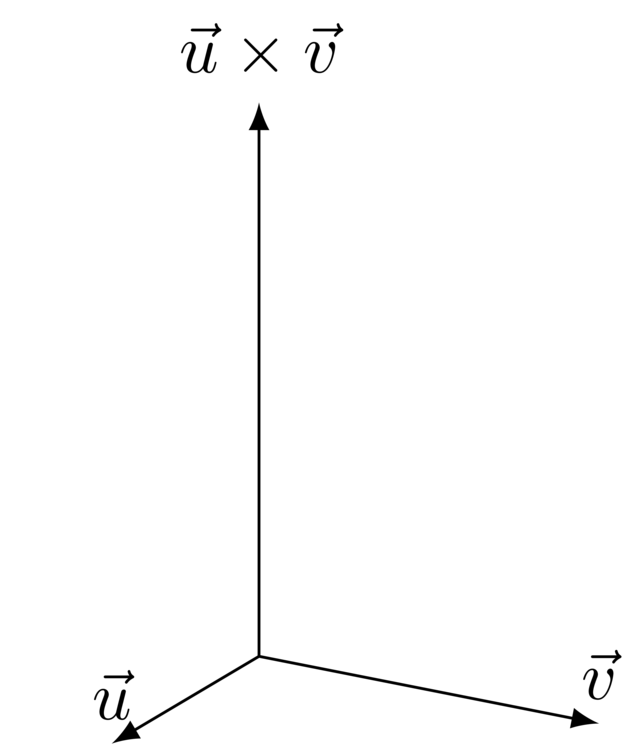
In this course, we will mostly rely on the first property: being able to find a vector that is perpendicular to two others will regularly come in handy.

There is one catch, though. Given two (nonparallel) vectors, there are always two vectors perpendicular to both. If some vector \(\vec p\) is perpendicular to both \(\vec u\) and \(\vec v\), then so is \(-\vec{p}\).

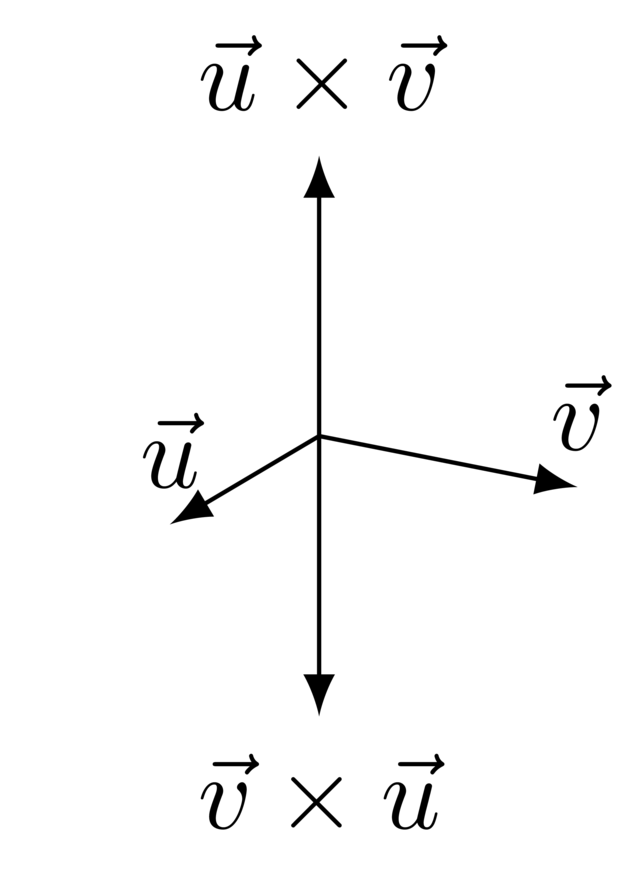
One perpendicular vector will be given by \(\vec u \times \vec v\), the other by \(\vec v \times \vec u\). It is very important to know which product yields which vector. This depends on the coordinate system used.

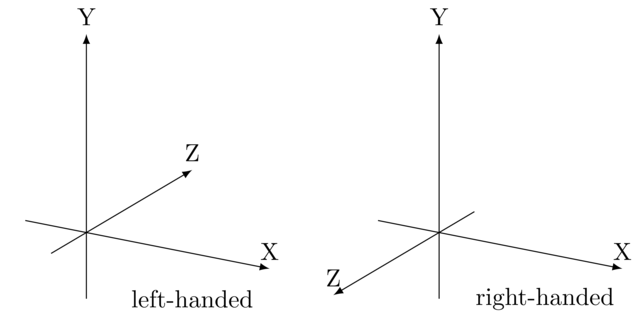
Say we position ourselves in front of the XY-axes so that X points right and Y points upwards. Then there are two possible choices for Z: either Z points away from us, or it comes towards us. If it points away, it is called a left-hand coordinate system, otherwise a right-hand coordinate system. The reasoning behind this naming goes as follows: let your thumb point in X-direction and your index in the Y-direction. Depending on which hand you used, your middle finger will then, if extended, either point towards you or away from you. This determines the Z-direction.

The cross product obeys the same rule: to find out which way \(\vec u \times \vec v\) points, align your thumb with \(\vec u\) and your index finger with \(\vec v\). Your middle finger then points in the same direction as \(\vec{u} \times \vec{v}\).

During this course, we will make use of right hand systems exclusively.