Refraction

' '

When a light ray reaches a transparent material, part of it penetrates the material, at which point the light ray is bent in another direction. The following explanation is not very exact, but it helps to understand refraction intuitively.

A light ray travels through a medium, for example air, water, glass, diamond, … Air is quite thin and photons can move through it mostly unhindered, meaning that a light beam travels through air at almost the speed of light. Diamonds, however, are very dense, making photons bump into carbon atoms all the time. As a consequence, a light beam is slowed down considerably, i.e. 2.42× slower than the "regular" speed of light.

You can imagine a light ray as photons flying next to each other:

When a car’s right wheels turn slower than its left wheels, the car will turn right. The same principle is true for the light ray. Consider the figure below. When the light ray reaches the new medium, say a denser one (so that it slows down), the lower photons arrive first and slow down while the upper photons still travel at full speed. This makes the ray make a right turn.

If the second medium were less dense, the lower photons would start moving faster while the upper are still going slowly, resulting in a left turn.

One way in which this explanation is faulty is that according to this model, if a photon were traveling alone, it would not bend, while in reality, it would.

1. Mathematics

1.1. Snell’s Law

Each transparent material is characterized by its refractive index \(n\). This index corresponds by the factor by which light is slowed down when it travels through the material. Examples of refractive indices are

Medium	Refractive Index
Vacuum	1
Air	1.000293
Water	1.3333
Glass	1.52

To determine how a light ray is bent when it changes from a medium with refractive index \(n_1\) to a medium with refractive index \(n_2\), we use Snell’s law.

\[ \frac{\sin \theta_1}{\sin \theta_2} = \frac{n_1}{n_2}\]

where \(\theta_1\) is the angle the light ray makes with the normal \(\vec n\) on the contact surface between the two materials.

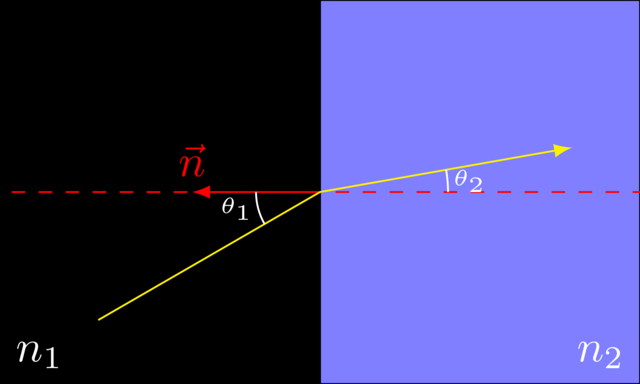
So, given the refractive indices \(n_1\) and \(n_2\), and the incoming angle \(\theta_1\), you can compute the outgoing angle \(\theta_2\):

\[ \theta_2 = \sin^{-1}\left(\frac{n_2}{n_1} \sin\theta_1\right)\]

There is one issue however: it is possible that \(\frac{n_2}{n_1} \sin\theta_1 > 1\), which makes it mathematically impossible to take the \(sin^{-1}\) as it is only defined for values between \(0\) and \(1\). What actually happens in this case is total internal reflection: instead of traversing the contact surface, the light ray will bounce off of it, as if it is a mirror.

1.2. Using Vectors

In its current form Snell’s law is not practical to use in our context. We rewrite it using vector math.

The algorithm needs the following inputs:

A unit vector \(\vec i\) representing the direction of the incoming light. This vector should point towards the origin of the ray.
The refractive indices of the materials \(n_1\) and \(n_2\).
The unit normal vector \(\vec n\) on the contact surface at the point where the light ray moves from the first to the second material.

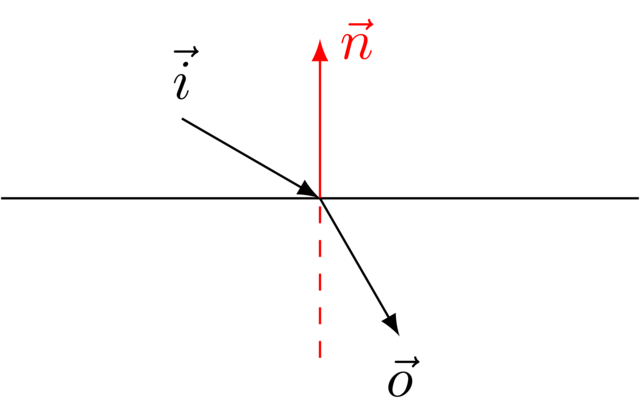
The outgoing direction of the ray can be found using the following formula:

\[ \begin{array}{rcl} \vec{o}_\mathrm{x} & = & \frac{n_1}{n_2} \cdot (\vec i - (\vec i \cdot \vec n) \cdot \vec n) \\ \vec{o}_\mathrm{y} & = & -\sqrt{1-|\vec{o}_\mathrm{x}|^2} \cdot \vec n \\ \vec{o} & = & \vec{o}_\mathrm{x} + \vec{o}_\mathrm{y} \\ \end{array}\]

You have to check whether \(1-|\vec{o}_\mathrm{x}|^2 < 0\). If this is the case, total internal reflection occurs. Note that \(|\vec{v}|\) denotes the length (also called norm) of the vector \(\vec{v}\).