Points and Vectors

' '

1. Definitions

A point is an infinitely small "dot" whose sole characteristic is its location in space. Two points at the same location are considered to be the same.

A vector is the difference between two points.

To differentiate between points and vectors, we’ll also use different naming conventions. Point names will consist of a single capital letter (\(P\), \(Q\), \(P_1\), …), whereas vectors shall be denoted using lowercase letters hatted with a fashionable arrow (\(\vec u\), \(\vec v\), …).

1.1. Analogy

Let us pick two numbers at random, say 5 and 9. If we wish to compute their difference, or the "distance" between them, we can subtract them, giving us 4, which is again a number. This means the difference between two numbers is a number.

Let us now pick two dates: 8 September 2000 and 18 September 2000. What is the "distance" between them? The difference is 10 days, which is obviously not a date. We can never express the difference between two dates as a new date: it makes no sense. Instead, the difference between two dates is a time span, or a duration.

A date is generally represented by three numbers, written day/month/year. A duration can be represented similarly: #days/#months/#years. So we could say that the difference between dates 8/9/2000 and 18/9/2000 is 10/0/0. Even though dates and durations can be expressed using three numbers, it is clearly absurd to interpret 10/0/0 as a date.

The same goes for points and vectors. A point corresponds to a date, whereas vectors correspond to durations. Given two points (4, 1, 9) and (4, 7, 6), the difference between them is the vector (0, 6, -3).

2. Specifying Points and Vectors

Both points and vectors can be specified using coordinates. There are multiple different coordinate systems:

Two dimensions
- 2D Cartesian
Polar
Three dimensions
- 3D Cartesian
- Spherical
- Cylindrical (TODO)

You are probably the most familiar with the Cartesian coordinate systems.

3. Visualization

Visually, a point is represented by a dot and a vector by an arrow.

Here, \(\vec v\) equals the difference between \(P\) and \(Q\): \(\vec v=Q-P\).

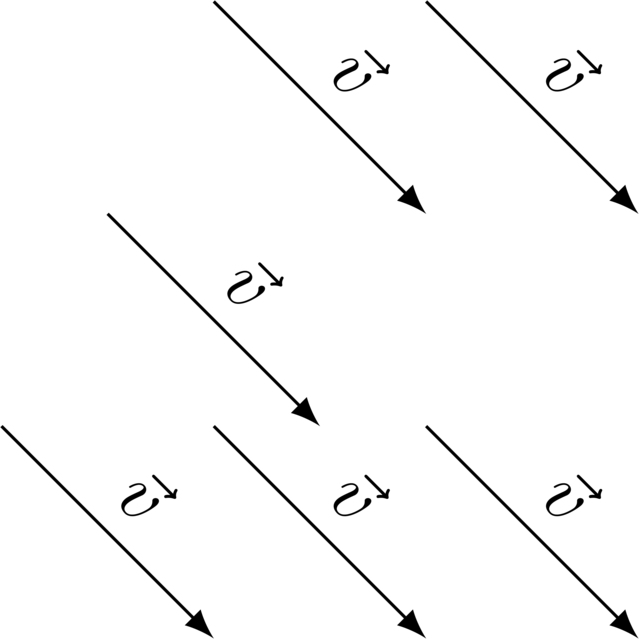
Realize that only the length, orientation and direction of the arrow have significance. All arrows below represent the same vector:

4. Operations on Points and Vectors

You are (hopefully) familiar with real numbers and the operators defined on them, such as addition, subtraction, multiplication, division, square root, etc. Similar operations are defined on points and vectors. However, you have to be careful to notice that not all combinations are permitted. For example, you can add two vectors, but you cannot add two points together.

4.1. Addition

Addition is defined for the following combinations of operand types:

Left operand	+	Right operand	=	Result
Vector	+	Vector	=	Vector
Point	+	Vector	=	Point
Vector	+	Point	=	Point

Left operand

Right operand

Result

Vector

Point

Vector

Point

Vector

Point

The addition can be computed using the following formula:

\[ \begin{array}{rclclr} (x_1, y_1) & + & (x_2, y_2) & = & (x_1 + x_2, y_1 + y_2) & \qquad\mathrm{(2D)} \\ (x_1, y_1, z_1) & + & (x_2, y_2, z_2) & = & (x_1 + x_2, y_1 + y_2, z_1 + z_2) & \qquad\mathrm{(3D)} \end{array}\]

The addition of two vectors corresponds to the combination of both displacements they represent.

The addition of a point \(P\) and a vector \(\vec v\) corresponds to the displacement of \(P\) in the direction designated by \(v\).

Notice that you cannot add two points together.

If you need to add points and vectors described in polar or spherical coordinates, you have to convert these into Cartesian coordinates first.

4.2. Subtraction

Subtraction is quite similar to addition. Again, take care of noticing which combinations of operands are allowed. The formula is what you would expect it to be:

\[ \begin{array}{rclclr} (x_1, y_1) & - & (x_2, y_2) & = & (x_1 - x_2, y_1 - y_2) & \qquad\mathrm{(2D)} \\ (x_1, y_1, z_1) & - & (x_2, y_2, z_2) & = & (x_1 - x_2, y_1 - y_2, z_1 - z_2) & \qquad\mathrm{(3D)} \end{array}\]

Following operands are allowed:

Left operand	-	Right operand	=	Result
Vector	-	Vector	=	Vector
Point	-	Vector	=	Point
Point	-	Point	=	Vector

Left operand

Right operand

Result

Vector

Point

Vector

Point

Vector

Point subtraction deserves a special mention: we’ll often rely on it to find the difference between points. The vector representing the difference between a point \(P\) and a point \(Q\) equals \(Q - P\).

The order is important: \(Q - P\) will bring you from \(P\) to \(Q\), whereas \(P - Q\) will take you from \(Q\) to \(P\). You can easily see this using the following math:

\[ P + (Q - P) = P + Q - P = P - P + Q = Q\]

whereas

\[ P + (P - Q)\]

cannot be simplified any further. \(P + P - Q = (P + P) - Q = 2 \cdot P - Q\) is not correct: it involves adding two points together, which is undefined.

4.3. Multiplication and Division

Multiplication is a bit more complex than addition and subtraction, as there are more possibilities. Vectors can both be multiplied by scalars (numbers) and other vectors. When multiplying vectors, there are two different ways of multiplying: the dot product with symbol \(\cdot\) and the cross product with symbol \(\times\).

Left operand		Right operand	=	Result
Vector	·	Vector	=	Scalar
Vector	×	Vector	=	Vector
Vector	·	Scalar	=	Vector
Scalar	·	Vector	=	Vector
Vector	/	Scalar	=	Vector

Left operand

Right operand

Result

Vector

Scalar

Vector

Scalar

Vector

Scalar

Vector

Scalar

Vector

4.3.1. Multiplication and Division By Scalars

Scalar is just a fancy name for "a number". Multiplying a vector \((x, y, z)\) with a scalar \(c\), written \((x, y, z) \cdot c\), results in a new vector:

\[ (x, y, z) \cdot c = c \cdot (x, y, z) = (c \cdot x, c \cdot y, c \cdot z)\]

i.e. you multiply each coordinate with the scalar.

Multiplication of a vector corresponds to lengthening (or shortening) the vector.

Notice the following:

Multiplying a vector by a scalar whose absolute value is greater than 1 lengthens the vector.
Multiplying a vector by a scalar whose absolute value is less than 1 shortens the vector.
Multiplying a vector by a negative number flips the vector around.

It is also possible to divide a vector by a scalar:

\[ \frac{\vec v}{c} = \vec v \cdot \frac1c\]

In other words, dividing a vector by 2 is the same as multiplying it by 1/2.

4.3.2. Multiplication With Two Vector Operands

As mentioned above, there are two ways to multiply two vectors: \(\vec u \cdot \vec v\) and \(\vec u \times \vec v\). Both these multiplications are important enough to deserve having their own page.

4.3.3. Norm of a Vector

The norm, size or length of a vector \(\vec v(x, y, z)\) can be computed with the follow formula:

\[ |\vec v| = \sqrt{\vec v \cdot \vec v} = \sqrt{x^2 + y^2 + z^2}\]

To find the distance between two points \(P\) and \(Q\), take the length of their difference:

\[ \mathrm{distance}(P, Q) = |Q-P|\]