Triangle

A triangle is uniquely defined by its three vertices \(P_1\), \(P_2\) and \(P_3\), so using only those three points we need to be able to find the intersection of the triangle with an arbitrary ray \(R(t) = O + \vec\Delta \cdot t\).

As explained earlier, our first goal is to find out where the ray \(R(t)\) hits the plane containing the triangle. The easiest way to go about this is relying on the following formula: say \(P\) is an arbitrary point on the plane and \(\vec N\) is a vector perpendicular on the plane, then if for a point \(H\)

then \(H\) lies on the plane. To be able to use this formula, we need a point \(P\) and vector \(\vec N\).

Finding a \(P\) is easy: we have three of them, namely the triangles vertices \(P_1\), \(P_2\) and \(P_3\). Any one of them will do. To find \(\vec N\), we need a little extra math.

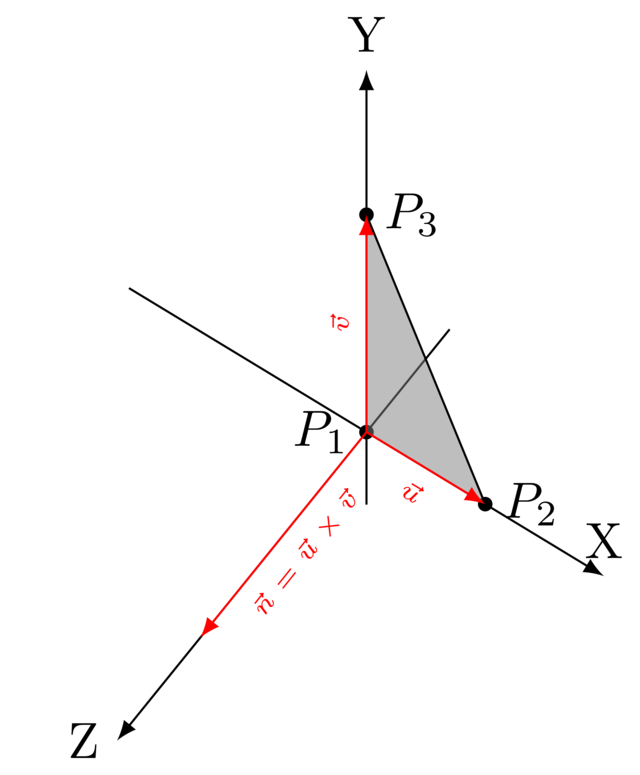
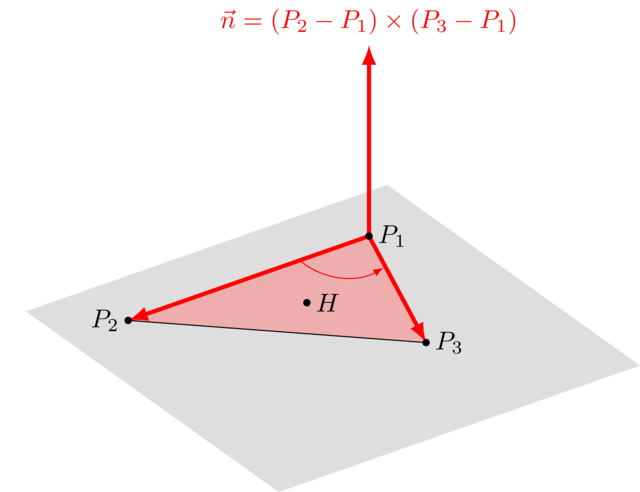
We compute \(\vec u = P_2 - P_1\) and \(\vec v = P_3 - P_1\). Both these vectors are in the plane. Taking their cross product \(\vec n = \vec u \times \vec v\) will yield a vector perpendicular on both of them, meaning it will also be perpendicular on the plane.

The formula above thus becomes

The point \(H\) should lie on the ray, i.e. \(H = O + \vec\Delta \cdot t\) for some \(t\). Plugging this into the equation gives

We only need to solve to \(t\) and we know where the ray hits the plane.

Now that we know where the hit \(H\) occurs between the ray and the plane containing the triangle, we still need to determine whether \(H\) lies within the bounds of the triangle.

Let’s say we stand at \(P_1\) and look at \(P_2\). \(H\) will be to the left of us. Next, let’s stand at \(P_2\) and look at \(P_3\). Again, \(H\) will be the to left of us. If we repeat this a last time, i.e. stand at \(P_3\) and look at \(P_1\), once again, \(H\) lies to the left.

So, if we can somehow determine to which side \(H\) lies with respect to a triangle’s side, we can find out if \(H\) lies inside the triangle.

Maybe the dot product can help us somehow. Let us investigate its sign. For the sake of clarity, we work in 2D. We take an arbitrary vector \(\vec v\) and draw it with its origin at \((0,0)\). Next, for each point \(P\) on the plane, we determine the vector \(\vec u = P - (0,0)\), i.e. we draw a vector from the origin to \(P\). Next, we compute the dot product \(\vec u \cdot \vec v\). Depending on whether the result is positive, zero or negative, we assign the point \(P\) the color green, blue or red, respectively.

As you can see, all points "in front of \(\vec v\)" are green and all points behind \(\vec v\) are red. In other words, the dot product can tell us whether a point lies before or behind us. But this does not help us with our triangle: we’d rather know whether a point is to the left or to the right of us.

Maybe the cross product can help. There’s a small problem though: the cross product yields vectors, not numbers, and there’s no such thing as the "sign of a vector". We’ll just have to draw the resulting vector then. More specifically, in each point \(P\) we draw the vector \(\vec v \times (P - O)\).

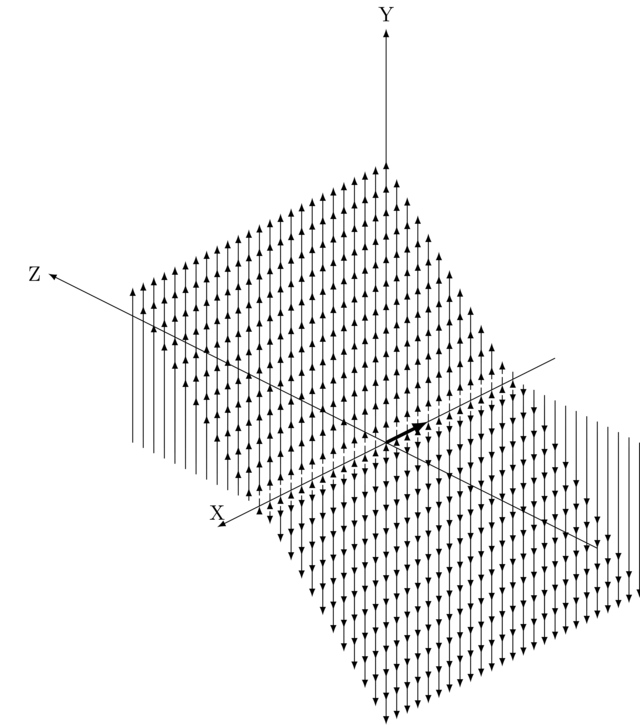
The result is quite interesting: the vectors to the left of \(\vec v\) point upwards and those to the right downwards. This makes sense: remember that with the cross product, the direction of the result depends on whether the angle between the operands goes clockwise or counterclockwise.

Consider the following figures:

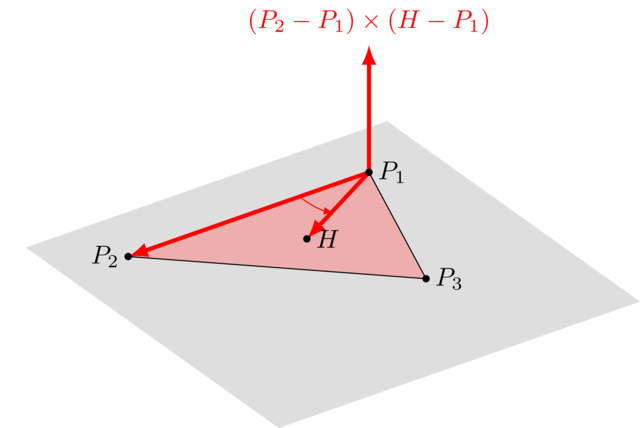
Say we stand at \(P_1\) and look at \(P_2\). We then turn slowly to \(P_3\). If while turning from \(P_2\) to \(P_3\) we encounter \(H\), it means \(H\) is on the right side of \(P_1P_2\). To define the "correct turning direction", we first compute \(P_1P_2 \times P_1P_3 = (P_2 - P_1) \times (P_3 - P_1)\). Next we compute \(P_1P_2 \times P_1H = (P_2 - P_1) \times (H-P_1)\). If both directions turn the same way (i.e. both clockwise or both counterclockwise), the cross product vectors will point in the same direction. We can detect this by relying on the dot product, which will be positive if this is the case. In short, \(H\) is on the correct side of \(P_1P_2\) if