Smooth Triangle

' '

Difficulty

Prerequisites

primitives/shapes/triangle

Reading material

design/primitives/ray-intersections

primitives/triangle

1. Problem Statement

Triangles are used to efficiently approximate complex shapes. Consider the wavy strip we created using triangles:

This is not a very convincing wavy strip: we can clearly see that it’s not truly wavy, but merely rectangles (which are built out of triangles but that is not visible) pretending to be. In order to make it appear smoother, we could increase the number of triangles:

Here, we doubled the amount of triangles, doubling the rendering time. Also, as you can see, the shading is still not perfectly smooth: there are visible jumps between the different shades of red. In this extension, we examine a cheaper way to make things look smoother without adding triangles:

2. Solution

For the sake of clarity, let’s switch to a 2D view: instead of using 3D triangles, we use 2D segments. Say we want to model the shape below using segments:

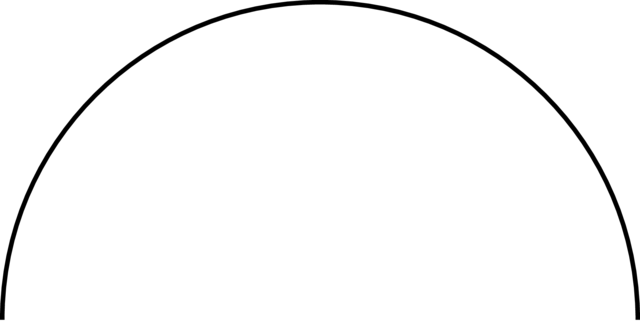
With four segments, we get the following approximation.

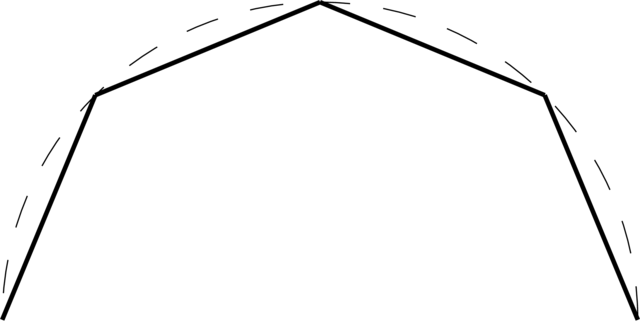
If we were to render this, we would clearly see that there are actually just four segments instead of a smooth curve. The reason we get discontinuities in the shading is due to the fact that segments are, well…, rather flat.

But what if we could somehow "bend" segments a bit?

2.1. Fake Normals

Consider the figure below. The arrows represent the normal vectors on the segments.

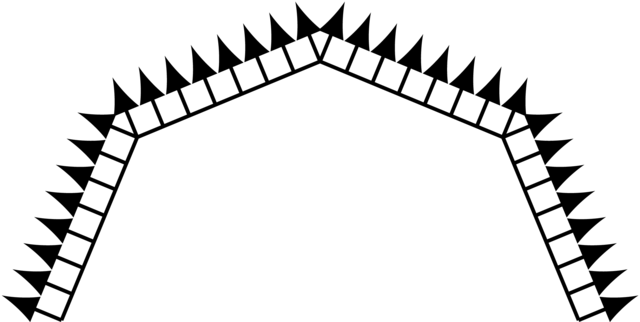
Since the segments are flat, all normals on the same segment point in the same direction. This normal is used by the shading algorithm (e.g., in ray tracer v2), which results in a "flat shading". What if we were to lie about the normals though?

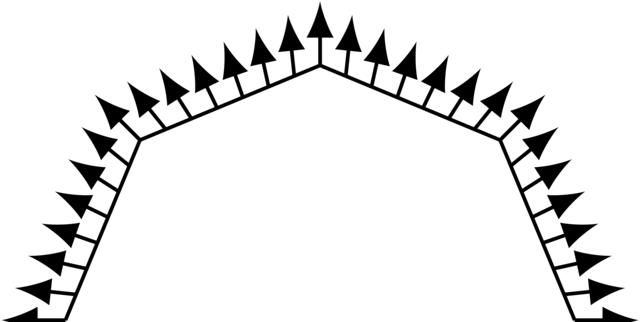
In this figure, the segments themselves are still their trusty flat selves. The normals, however, gently rotate. In fact, we "transplanted" the normals from the circle to the segments.

If we were to render the same principle in 3D, we would get much smoother results.

2.2. 2D Interpolation

Given a segment, it is easy to find its intersection with a ray. But we still need to compute the normal at that intersection.

In the previous section, we stole them from the shape the segments approximated. We can still do this, but computing this would still be rather expensive, and the whole point of using segments is to speed things up.

When we define a segment, we obviously need to specify its endpoints. Let’s say that we must also provide the normals at these endpoints:

Primitive smooth_segment(const Point2D&  endpoint1,
                         const Vector2D& normal1,
                         const Point2D&  endpoint2,
                         const Vector2D& normal2)
{
    // ...
}

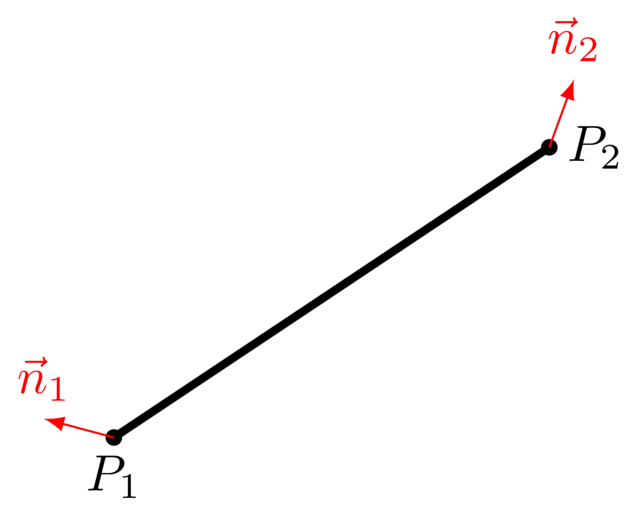
Given this extra information, we can interpolate the normal. If the ray intersects the segment at some point \(P\), we need to determine the normal \(\vec{n}\) at this point \(P\). We can proceed as follows:

If \(P = P_1\), we should use \(\vec{n}_1\) as our normal.
If \(P = P_2\), we should use \(\vec{n}_2\) as our normal.
If \(P\) is located in the middle of the segment, we should "mix" both normals \(\vec{n}_1\) and \(\vec{n}_2\). We can take the average of both: \(\vec{n} = (\vec{n}_1 + \vec{n}_2) / 2\).

Generally, we can say that

The closer \(P\) is to \(P_1\), the more \(\vec{n}\) should equal \(\vec{n}_1\).
The closer \(P\) is to \(P_2\), the more \(\vec{n}\) should equal \(\vec{n}_2\).

Mathematically, we need to find some values \(\alpha\) and \(\beta\) that expresses how close to \(P_1\) or \(P_2\) some point \(P\) is:

\[\alpha = \frac{|P_2-P|}{|P_2-P_1|} \qquad \beta = 1 - \alpha\]

When \(P=P_1\), we get \(\alpha = 1\) and \(\beta=0\). When \(P=P_2\), we get \(\alpha = 0\) and \(\beta=1\). Using this, we can compute the normal:

\[\vec{n} = \frac{\alpha \cdot \vec{n}_1 + \beta \cdot \vec{n}_2}{|\alpha \cdot \vec{n}_1 + \beta \cdot \vec{n}_2|}\]

2.3. 3D Interpolation

The same trick can be applied in 3D to triangles: each vertex is also given a normal.

Primitive smooth_triangle(const Point3D&  vertex1,
                          const Vector3D& normal1,
                          const Point3D&  vertex2,
                          const Vector3D& normal2,
                          const Point3D&  vertex3,
                          const Vector3D& normal3)
{
    // ...
}

Given a point \(P\), we need to know how far it is from the three vertices \(P_1\), \(P_2\) and \(P_3\), expressed by three values \(\alpha\), \(\beta\) and \(\gamma\). Computing the normal at \(P\) can then be done using the formula

\[\vec{n} = \frac{\alpha \cdot \vec{n}_1 + \beta \cdot \vec{n}_2 + \gamma \cdot \vec{n}_3}{|\alpha \cdot \vec{n}_1 + \beta \cdot \vec{n}_2 + \gamma \cdot \vec{n}_3|}\]

Look online for how to compute \(\alpha\), \(\beta\) and \(\gamma\).

Tip	Barycentric coordinates.

3. Implementation

Create files primitives/smooth-triangle-primitive.cpp and primitives/smooth-triangle-primitive.h. Copy paste the implementation of (flat) triangles and make the necessary changes.

As a reminder, the factory function should have as signature

Primitive smooth_triangle(const Point3D&  vertex1,
                          const Vector3D& normal1,
                          const Point3D&  vertex2,
                          const Vector3D& normal2,
                          const Point3D&  vertex3,
                          const Vector3D& normal3)

4. Evaluation

Render the scene below:

def f(x, z) {
  var y = 0.2 * sin(degrees(360) * x)
  pos(x, y, z)
}

def fn(x, y) {
  var sx = -0.2 * 2 * 3.141592 * cos(degrees(360) * x)

  vec(sx, 1, 0).normalized()
}

def scene_at(now)
{
  var camera = Cameras.perspective( [ "eye": pos(5, 5, 5),
                                      "look_at": pos(0,0,0) ] )

  var triangles = []

  var dx = 0.1
  var dy = dx

  for ( var x = -2.0; x <= 2.0; x += dx ) {
    for ( var y = -2.0; y <= 2.0; y += dy ) {
      var p1 = f(x, y)
      var p2 = f(x + dx, y)
      var p3 = f(x, y + dy)
      var p4 = f(x + dx, y + dy)
      var n1 = fn(x, y)
      var n2 = fn(x + dx, y)
      var n3 = fn(x, y + dy)
      var n4 = fn(x + dx, y + dy)

      triangles.push_back(smooth_triangle(p1, n1, p2, n2, p3, n3));
      triangles.push_back(smooth_triangle(p2, n2, p3, n3, p4, n4))
    }
  }

  var material = Materials.uniform([ "ambient": Colors.red() * 0.1, "diffuse": Colors.red() ])

  var root = decorate(material, union(triangles))

  var lights = [ Lights.omnidirectional( pos(0, 5, 0), Colors.white() ) ]

  create_scene(camera, root, lights)
}

var raytracer   = Raytracers.v2()

var renderer    = Renderers.standard( [ "width": 500,
                                        "height": 500,
                                        "sampler": Samplers.single(),
                                        "ray_tracer": raytracer ] )

pipeline( scene_at(epoch()),
          [ Pipeline.renderer(renderer),
            Pipeline.studio() ] )